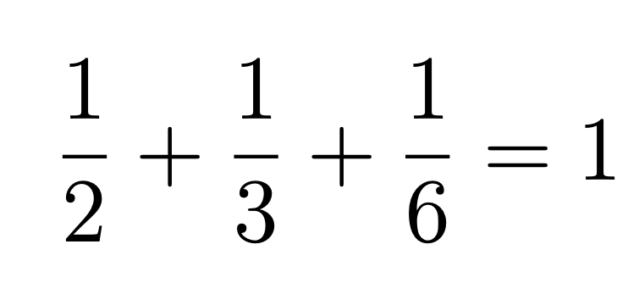Problem of the Week: Seeking Unity
Editor’s Note: The Department of Mathematics at Gettysburg College hosts a problem of the week challenge to determine each semester’s Paul Mugabi problem-solving award recipient(s). Each week’s entries are scored by a faculty judge, and winner(s) from each week will receive a Problem Of the Week (P.O.W.) button. The Gettysburgian is not involved in or responsible for accepting or evaluating students’ submissions to this contest.
THE RULES:
The contest is open to all Gettysburg College students. Up to three people may work together on a submission. Make sure your name is on your submission and that any sources are properly cited. Send solutions to bkennedy@gettysburg.edu. This problem was posted on Thursday, March 31 and solutions are due on Friday, April 8 by 5:00 p.m.
THE PROBLEM:
Let us say that a set of positive whole numbers achieves unity if the numbers are all different and the sum of their reciprocals is equal to one. For example, the set of three numbers 2, 3, and 6 achieves unity because the numbers are all different and
QUESTION:
Find a set of four positive whole numbers that achieves unity.
Bonus: Find all possible sets of four positive whole numbers that achieve unity.
Extra Bonus: Explain how you know your list of such sets is complete.