Problem of the Week: Chase!
Editor’s Note: The Department of Mathematics at Gettysburg College hosts a problem of the week challenge to determine each semester’s Paul Mugabi problem-solving award recipient(s). Each week’s entries are scored by a panel of faculty judges, and winner(s) from each week will receive a Problem Of the Week (P.O.W.) button. The Gettysburgian is not involved in or responsible for accepting or evaluating students’ submissions to this contest.
THE RULES:
The contest is open to all Gettysburg College students. Up to three people may work together on a submission. Make sure your name is on your submission and that any sources are properly cited! Send solutions to bkennedy@gettysburg.edu or put solutions in the marked envelope in the hallway outside Glatfelter 215. This problem was posted on Friday, January 25 and solutions are due on Friday, February 1 by 5:00 p.m.
THE PROBLEM:
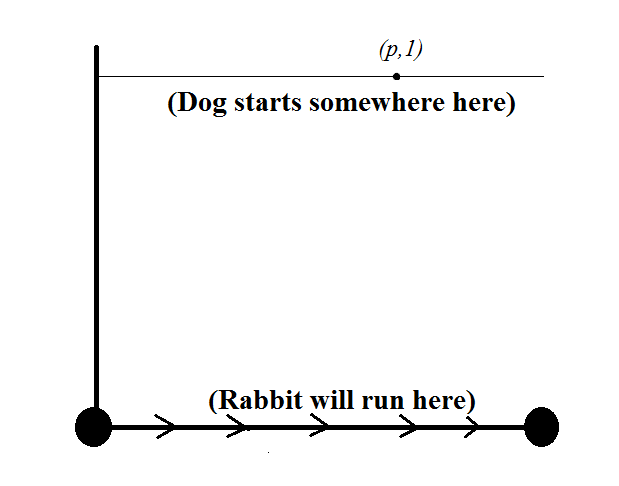
A rabbit is going to come out of its hole (located at point (0,0) in the plane) at time t = 0 and run in a straight line, at speed 1, to another hole located at point (1, 0) in the plane.
At time t = 0, a dog is standing at point (p, 1) in the plane, where 0 ≤ p ≤ 1. While the rabbit runs, the dog chases it. The dog runs at constant speed r > 0 and always runs directly toward the rabbit.
QUESTION: Say as much as you can about what values of p and r allow the dog to catch the rabbit. Solutions that include computer-aided investigations are encouraged!