Problem of the Week: Cutting Up
The Math Department’s Problem of the Week for September 7-14
Editor’s Note: The Department of Mathematics at Gettysburg College hosts a problem of the week challenge to determine each semester’s Paul Mugabi problem-solving award recipient(s). Each week’s entries are scored by a panel of faculty judges, and winner(s) from each week will receive a Problem Of the Week (P.O.W.) button. The Gettysburgian is not involved in or responsible for accepting or evaluating students’ submissions to this contest.
THE RULES:
The contest is open to all Gettysburg College students. Up to three people may work together on a submission. Make sure your name is on your submission and that any sources are properly cited! Send solutions to bkennedy@gettysburg.edu or put solutions in the marked envelope in the hallway outside Glatfelter 215. This problem was posted on Friday, September 7 and solutions are due on Friday September 14 by 5:00 p.m.
THE PROBLEM:
Recall that a polygon is convex if any two points inside it can be connected by a straight line that lies entirely inside the polygon (the polygon has no “indentations”).
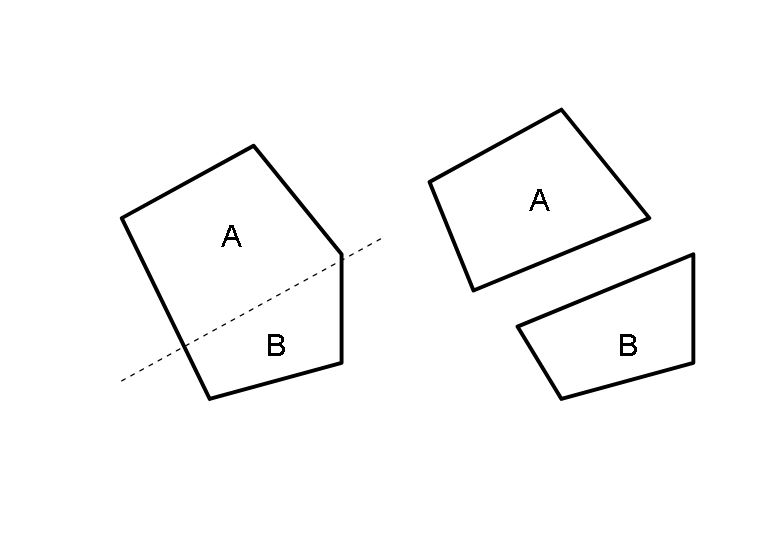
If C is a convex polygon, drawing a straight line through it cuts C into two new polygons A and B, as in the figure below.
Can you find a convex polygon C (not necessarily regular!) and a straight line cutting through C so that one of the two new polygons created by the cut (let’s call it A) has the following properties?
- The area of A is precisely half the area of C.
- The perimeter of A is precisely half the perimeter of C.
[Hint: form C by putting a rectangle and a triangle together.]
